What Does Slope Rating Mean in Golf

Understanding The Linear Regression!!!!

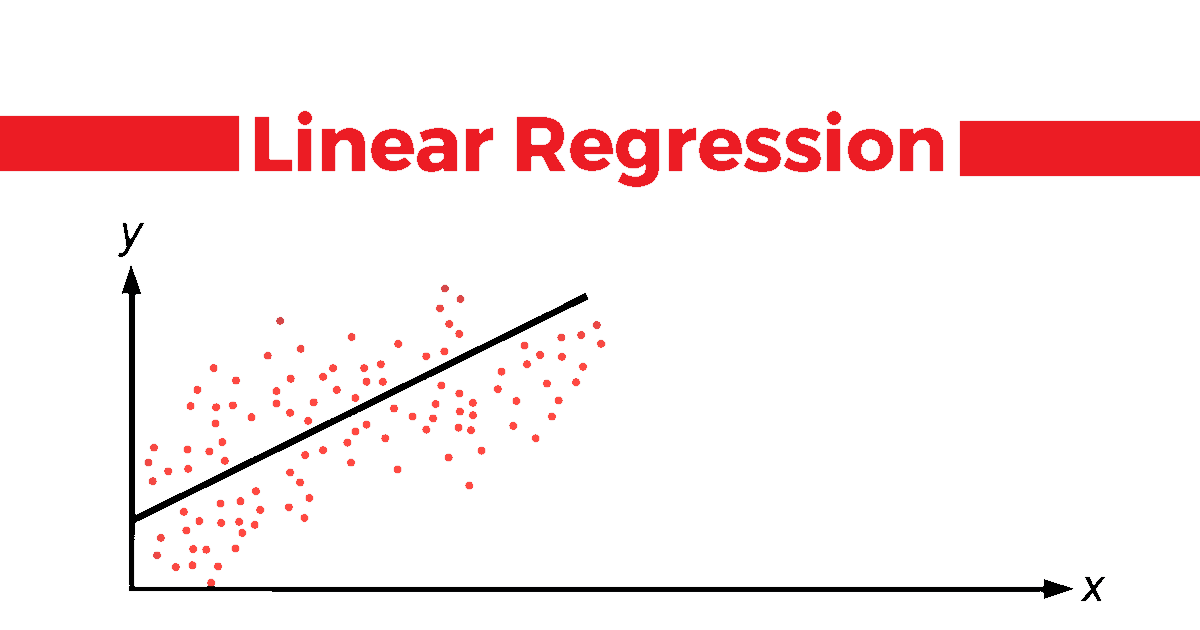
Everyone new to the field of data science or machine learning,often starts their journey by learning the Linear Models of the vast set of Algorithm's available.
So,Let's Start!!!

Content:

What is Linear Regression?
Assumptions of Linear Regression.
Types of Linear Regression?
Understanding Slopes and Intercepts.
How does a linear Regression Work?
What is a Cost Function?
Linear Regression with Gradient Descent.
Interpreting the Regression Results.

What is Linear Regression?

Linear Regression is a statistical supervised learning technique to predict the quantitative variable by forming a linear relationship with one or more independent features.
It helps determine:
→ If a independent variable does a good job in predicting the dependent variable.
→ Which independent variable plays a significant role in predicting the dependent variable.

Now,As you know most of the algorithm works with some kind of assumptions.So, Before moving on here is the list of assumptions of the Linear Regression.
These assumptions should be kept in mind when performing Linear Regression analysis so that the model performs it's best.

Assumptions of Linear Regression:

The Independent variables should be linearly related to the dependent variables.
This can be examined with the help of several visualization techniques like: Scatter plot or maybe you can use Heatmap or pairplot(to visualize every features in the data in one particular plot).
Every feature in the data is Normally Distributed.
This again can be checked with the help of different visualization Techniques,such as Q-Q plot,histogram and much more.
There should be little or no multi-collinearity in the data.
The best way to check the prescence of multi-collinearity is to perform VIF(Variance Inflation Factor).
The mean of the residual is zero.
A residual is the difference between the observed y-value and the predicted y-value.However, Having residuals closer to zero means the model is doing great.
Residuals obatined should be normally distributed.
This can be verified using the Q-Q Plot on the residuals.
Variance of the residual throughout the data should be same.This is known as homoscedasticity.
This can be checked with the help of residual vs fitted plot.
There should be little or no Auto-Correlation is the data.
Auto-Correlation Occurs when the residuals are not independent of each other.This usally takes place in time series analysis.
You can perform Durbin-Watson test or plot ACF plot to check for the autocorrelation.If the value of Durbin-Watson test is 2 then that means no autocorrelation,If value < 2 then there is positive correlation and if the value is between >2 to 4 then there is negative autocorrelation.

If the features in the dataset are not normally distributed try out different transformation techniques to transform the distribution of the features present in the data.

Can you say,why these assumptions are needed?

The Gauss-Markov theorem states that if your linear regression model satisfies the first six classical assumptions, then ordinary least squares ( OLS ) regression produces unbiased estimates that have the smallest variance of all possible linear estimators.

To Read More about the theorem please go to this link.

Now that few things are Clear let's move on!!!

Types of Linear Regression

→ Simple Linear Regression:

Simple Linear Regression helps to find the linear relationship between two continuous variables,One independent and one dependent feature.
Formula can be represented as y=mx+b or,

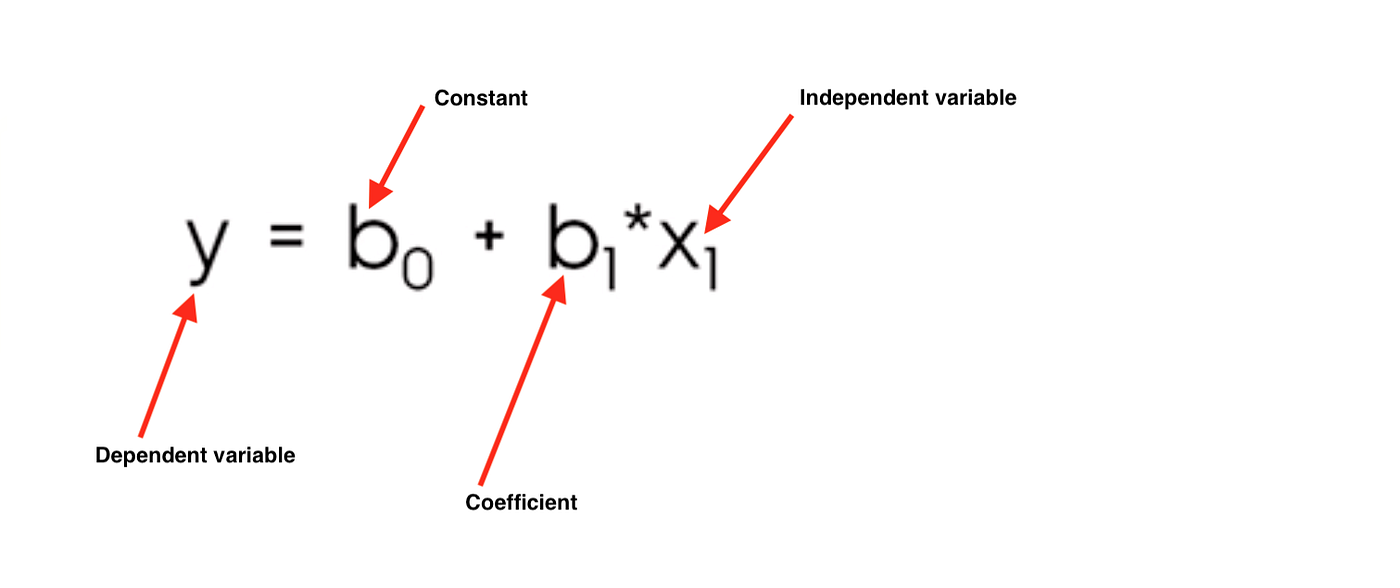
→ Multiple Linear Regression:

Multiple linear Regression is the most common form of linear regression analysis. As a predictive analysis, the multiple linear regression is used to explain the relationship between one continuous dependent variable and two or more independent variables.
The independent variables can be continuous or categorical (dummy coded as appropriate).
We Often use Multiple Linear Regression to do any kind of predictive analysis as the data we get has more than 1 independent features to it.
Formula can be represented as Y=mX1+mX2+mX3…+b ,Or

Now that we know different types of linear regression,Let's understand how the slope co-efficients and y-intercept are calculated.

let's look below to understand what slope and intercept is.

From,Here on we'll understand the concept with the help of,

Simple Linear Regression.

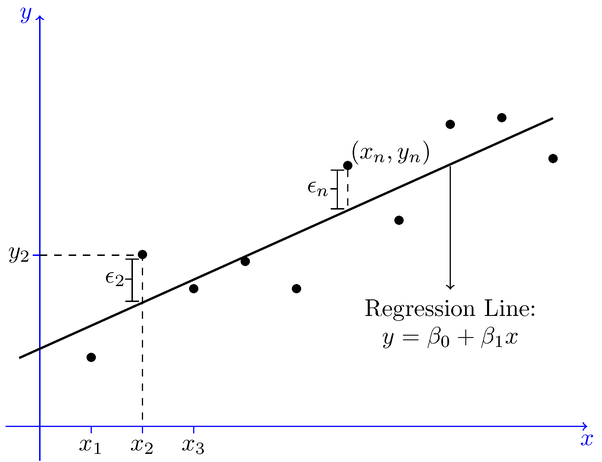
Understanding the Slope and intercept in the linear regression model:

What is a slope?
In a regression context, the slope is very important in the equation because it tells you how much you can expect Y to change as X increases.
It is denoted by m in the formula y = mx+b.

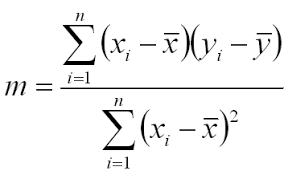
It can also be calculated by the formula,

m = r*(Sy/Sx),
Where r is the correlation co-efficient.
Sy and Sx is the standard deviation of x and y.
And r can be calculated as

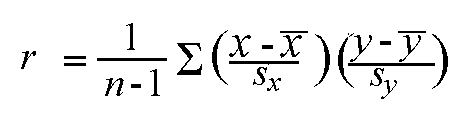
What is Intercept?
The y-intercept is the place where the regression line y = mx + b crosses the y-axis (where x = 0), and is denoted by b.
Formula to calculate the intercept is:

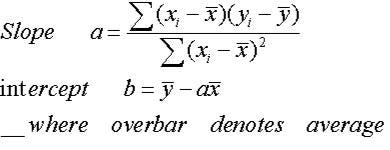
Now,Put this slope and intercept into the formula (y = mx +b) and their you have the description of the best fit line.

This best fit line will now pass through the data according to the properties of a regression line that is discussed below.Now,What if i tell you there is still room to improve the best fit line?
As you know, we want our model to be the best performing model on unseen data and to do so Stochastic Gradient Descent is used to update the values of slope and intercept,so that we acheive very low cost function of the model.
Don't worry we will look into it later in this blog.

How does a linear Regression Work?

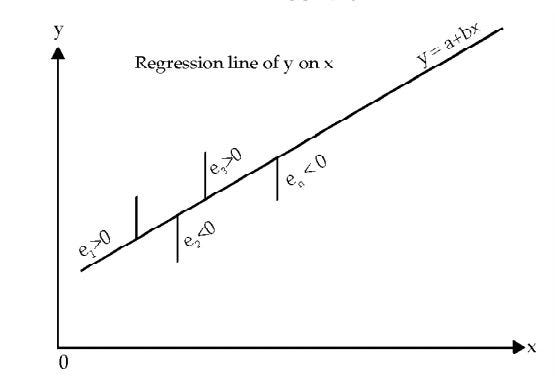
The whole idea of the linear Regression is to find the best fit line,which has very low error(cost function).
This line is also called Least Square Regression Line(LSRL).

The line of best fit is described with the help of the formula y=mx+b.
where,m is the Slope and
b is the intercept.

Properties of the Regression line:
1. The line minimizes the sum of squared difference between the observed values(actual y-value) and the predicted value(ŷ value)
2. The line passes through the mean of independent and dependent features.

Let's Understand what cost function(error function) is and how gradient descent is used to get a very accurate model.

Cost Function of Linear Regression

Cost Function is a function that measures the performance of a Machine Learning model for given data.
Cost Function is basically the calculation of the error between predicted values and expected values and presents it in the form of a single real number.
Many people gets confused between Cost Function and Loss Function,
Well to put this in simple terms Cost Function is the average of error of n-sample in the data and Loss Function is the error for individual data points.In other words,Loss Function is for one training example,Cost Function is the for the entire training set.

So,When it's clear what cost function is Let's move on.

The Cost Function of a linear Regression is taken to be Mean Squared Error.
some.People may also take Root Mean Square Error.Both are basically same,However adding a Root significantly reduces the value and makes it easy to read.We,take Square here so that we don't get values in negative.

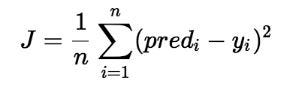
Here, n is the total number of data in the dataset.

You must be wondering where does the slope and intercept comes into play here!!

          J = 1/n*sum(square(pred - y))          Which, can also be written as :          J = 1/n*sum(square(pred-(mx+b)))  i.e, y = mx+b

We want the Cost Function to be 0 or close to zero,which is the best possible outcome one can get.
And how do we acheive that?
Let's Look at the gradient descent and how it helps improve the weights(m and b) to achieve the desired cost function.

Linear Regression with Gradient Descent

Gradient descent is an optimization algorithm used to find the values of parameters (coefficients) of a function that minimizes a cost function (cost).

To Read more about it and get a perfect understanting of Gradient Descent i suggest to read Jason Brownlee's Blog.

To update m and b values in order to reduce Cost function (minimizing MSE value) and achieving the best fit line you can use the Gradient Descent. The idea is to start with random m and b values and then iteratively updating the values, reaching minimum cost.

Steps followed by the Gradient Descent to obtain lower cost function:

→ Initially,the values of m and b will be 0 and the learning rate(α) will be introduced to the function.
The value of learning rate(α) is taken very small,something between 0.01 or 0.0001.

The learning rate is a tuning parameter in an optimization algorithm that determines the step size at each iteration while moving toward a minimum of a cost function.

→ Then the partial derivative is calculate for the cost function equation in terms of slope(m) and also derivatives are calculated with respect to the intercept(b).After Calculation the equation acheived will be.

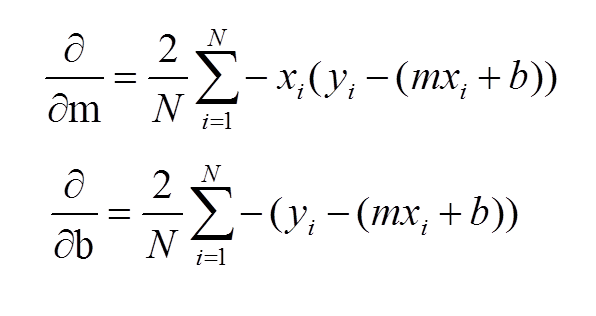
Guys familiar with Calculus will understand how the derivatives are taken.

If you don't know calculus don't worry just understand how this works and it will be more than enough to think intuitively what's happening behind the scenes and those who want to know the process of the derivation check out this blog by sebastian raschka.

→ After the derivatives are calculated,The slope(m) and intercept(b) are updated with the help of the following equation.
m = m+α*derivative of m
b = b+α*derivative of b
derivative of m and b are calculated above and α is the learning rate.

You must be wondering why I added and not subtracted,Well if you observe the result of the derivative you will see that the result is in negative.So the equation turns out to be :

m = m — α*derivative of m

b = b — α*derivative of b

If you've gone through the Jason Brownlee's Blog you might have understood the intuition behind the gradient descent and how it tries to reach the global optima(Lowest cost function value).

Why should we substract the weights(m and b)with the derivative?
Gradient gives us the direction of the steepest ascent of the loss function and the direction of steepest descent is opposite to the gradient and that is why we substract the gradient from the weights(m and b)

→ The process of updating the values of m and b continues until the cost function reaches the ideal value of 0 or close to 0.
The values of m and b now will be the optimum value to describe the best fit line.

I hope things above are making sense to you.So,Now let's understand other important things related to the linear Regression.

Till now we have understood How the Slope(m) and Intercept(b) are calculated,what Cost Function is and How Gradient Descent algorithm helps get the ideal Cost Function Value with the help of Simple Linear Regression.
For Multiple Linear Regression everything happens exactly same just the formula changes from a simple equation to a bigger one as shown above.

Now to understand How Co-efficients are calculated in Multiple Linear Regression, please go to this link to get a brief idea about it , Although you won't be performing it manually ,but, it's always good to know what's happening behind the scene.

Now Let's Look at how to check the quality of the model.

Interpreting the results of Linear Regression:

Photo by National Cancer Institute on Unsplash

You have cleaned the data and passed it on to the model,Now the question arises, How do you know if your Linear Regression Model is Performing well?

For That we Use the Statsmodel Package in Python and After fitting the data we do a .Summary() on the model,which gives result as shown in the pic below.(P.S. — I used a pic from google images)

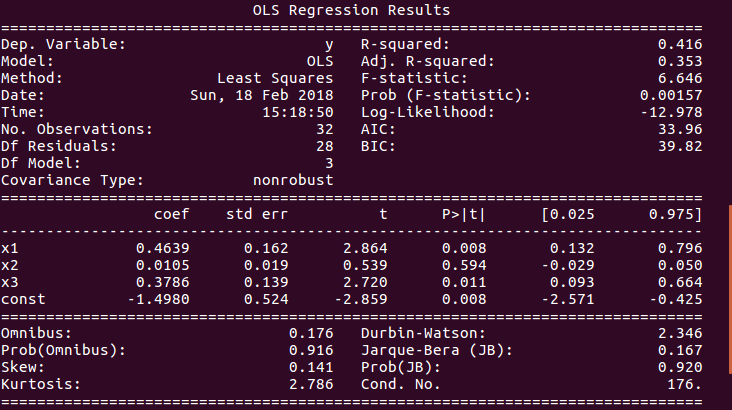
Now,If you Look at the Pic Carefully you will see a bunch of different Statistical test.
I Suppose you are familiar with R-Squared and Adjusted R-Squared shown on the top right of the image,If you don't no worries read my blog about R-Squared and P-value.

Here we will see what the lower block of the image interprets.

Omnibus/Prob(Omnibus):It is statistical test that tests the skewness and Kurtosis of the residual.
A value of Omnibus close to 0 show the normalcy(normally distributed) of the residuals.
A value of Prob(Omnibus) close to 1 show the probability that the residuals are normally distributed.
Skew: It is a measure of the symmetry of data,values closer to 0 indicates the residual distribution is normal.
Kurtosis: It is a measure of whether the data are heavy-tailed or light-tailed relative to a normal distribution. That is, data sets with high kurtosis tend to have heavy tails, or outliers. Data sets with low kurtosis tend to have light tails, or lack of outliers.
Greater Kurtosis can be interpreted as a tighter clustering of residuals around zero, implying a better model with few outliers.
Durbin-Watson:It is a statistical test to detect any auto-correlation at a lag 1 present in the residuals.
→ value of test is always between 0 and 4
→ IF value = 2 the there is no auto-correlation
→ IF value greater than(>) 2 then there is negative auto-correlation,which means that the positive error of one observation increases the chance of negative error of another observation and vice versa.
→ IF value less than(<) 2 the there is positive auto-correlation.
Jarque-Bera/Prob(Jarque-Bera):It is a Statistical test which test a goodness of fit of whether the sample data has skewness and kurtosis matching the normal distribution.
Prob(Jarque-Bera) indicates normality of the residuals.
Condition Number:This is a Statistical Test that measures the sensitivity of a function's output as compared to its input.
When there is multicollinearity present , we can expect much higher fluctuations to small changes in the data,So the value of the test will be very high.
A lower value is expected,something below 30,or more specifically value closer to 1.

I hope this article helped you understand the Algorithm and Most of the concepts related to it.
Coming up next Week,We will Understand the Logistic Regression.

HAPPY LEARNING!!!!!

Source: https://medium.com/analytics-vidhya/understanding-the-linear-regression-808c1f6941c0

Posted by: nicollgrequitairs.blogspot.com

What Does Slope Rating Mean in Golf